Números pedriscos, Algoritmo de números naturales

Historia de los grafos

El origen de la teoría de grafos se remonta al siglo XVII con el problema de los puentes de Königsberg, el cual consistía en encontrar un camino que recorriera los siete puentes del Rio Pregel en la ciudad de Königsberg, actualmente Kaliningrado, de modo que se recorrieran todos los puentes pasando una sola vez por cada uno de ellos.

                El primer resultado de un trabajo sobre la temática de grafos es la de Leonhard Euler el cual trato de conseguir una solución sobre el problema planteado. También se considera como uno de los primeros resultados topológicos en geometría. A la conclusión que llego Euler fue la construcción de teoremas que exponían que no era posible recorrer los sietes puentes amenos que estos (representados como vértices) presenten un grado par (el grado de un grafo es la cantidad de aristas que concurren al mismo).

      Un grafo, es una estructura matemática que permite modelar problemas de la vida cotidiana, mediante, una representación gráfica formada por nodos o vértices que muestra a los actores y aristas que sirven para representar los lazos o relaciones entre los actores.

GRAFO

                Vamos a definir a un grafo como un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones entre elementos de un conjunto. Típicamente, un grafo se representa gráficamente como un conjunto de puntos unidos por líneas. La unión de un vértice con otro es bidireccional, de forma tal que el subconjunto {a,b}  es lo mismo que {b,a}.

G=(V,E).

V= Conjunto de vértices

E= Conjunto de aristas

¿Qué es un Dígrafo?

                Un dígrafo posee las mismas características de un grafo con la diferencia de que las aristas entre sus vértices se definen como pares ordenados, de tal forma que la arista (a,b) no puede ser tomado como una igualdad con el par ordenado (b,a).

Calificacion de Grafos:

-          Camino: Sean X e Y (no necesariamente distintos) de un grafo no dirigido G=(V,E).

Un camino X-Y en G es una secuencia de vértices finita tal que exista una arista entre cada vértice y el siguiente. Además de esto no hay lazos (arista que conecta un vértice al mismo vértice). Si dentro del camino ningún vértice se repite el grafo se define como un camino simple.

Dentro de esto podemos decir que:

La Longitud es el número de n aristas que hay en el camino y dentro del camino se pueden repetir aristas y vértices.

-          Recorrido: Definido un camino X-Y, el mismo se puede definir como una recorrido o trayectoria si existe una sucesión finita de vértices unidas por aristas de tal forma que en el conjunto de arista no se seleccione mas de una vez cada arista.

-          Una vez definido un Camino que es Recorrido diremos que el mismo es un circuito si es cerrado. Esto quiere decir que el punto inicial será un vértice V y el punto final será el mismo vértice.  

-          Grafo conexo: Un grafo será conexo si existe un camino simple entre cualquiera dos vértices distintos de grafo G=(V,E). En caso contrario el grafo se denomina como un grafo no conexo (o disconexo) en el cual las diferentes partes conexas son los componentes de la grafica.

                             

Por último, veremos calificaciones que se lograron construir gracias a Leonhard Euler.

Recorrido Euleriano:

Definido un camino X-Y que sea abierto y que pase por todas las aristas, sin que se repita ninguna, se denomina como un recorrido Euleriano.

               También diremos que si un recorrido presenta mas de dos vértices de grados impar entonces no existe un recorrido Euleriano y, en otro caso, si existe únicamente dos vértices de grados impar entonces si es posible la construcción de un recorrido de Euler

Circuito Euleriano:

Definido un recorrido cerrado X-X que pase por todas las aristas, sin que estas se repitan, se denominara como circuito Euleriano.

               Podemos decir que si un recorrido posee un vértice de grado impar no será capaz de presentar un circuito Euleriano y, en el otro caso, si todos los vértices poseen grado par entonces si existe un circuito de Euler.

GRAFO PONDERADO

Definido un grafo G(V,E), llamaremos grafo ponderado a G si las aristas existentes poseen números. Es decir, si la arista e se etiqueta k entonces el peso de la arista e es k. De forma tal que las aristas poseen valores, y, la longitud de una trayectoria es una gráfica ponderada es la suma de los pesos de las aristas de las trayectorias.

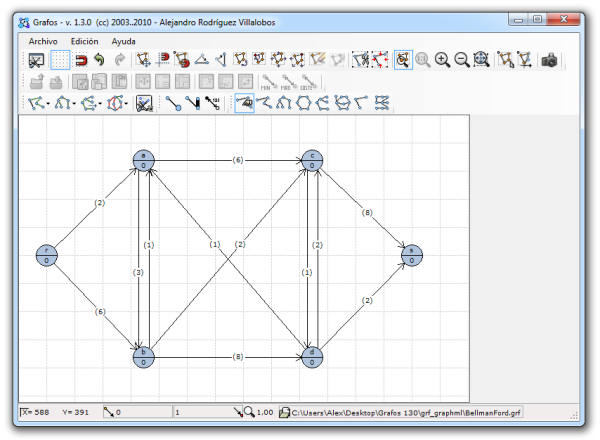
Software GRAFOS:

Un programa útil para la construcción de grafos (o dígrafos) es el programa GRAFOS. El mismo presenta la posibilidad de representar los datos en forma de selección de los usuarios (es decir que el usuario construye su propio grafo a gusto) o también existe la posibilidad la posibilidad de asignar diferentes valores a través de matrices. Cualquiera sea el caso tenemos la posibilidad de asignar valor a los nodos, un valor mínimo y máximo a las aristas, también podemos asignarle costos y etiquetas.

                Ademas de todo esto también posee las herramientas para utilizar diferentes algoritmos como el de Dikstra, y en el caso de construccion de árboles, Primm y Kruskal